ちょっとやってみたこと
┗
X+Y-Z＝D-1


■ 突然ですが、「円」及び「球」以外の図形において「頂点＋面-辺＝次元-1」という式が成り立つことをご存知ヵ？

このページの題名である「X+Y-Z＝D-1」は、Ｘは「頂点」、Ｙは「面」、Ｚは「辺」、Ｄは「次元」を意味します。
ここではこの式が成り立つのか、図を使って確認してみたいと思います。
■ 私は小学校2年の頃、日々平面図形に向かって自分なりにいろいろと不完全な公式を導きして遊んでいました（一時的なものでしたが）。それからしばらくしてそんな遊びもすることなかったのですっかり忘れていたのですが、さきほどの式をある本で見た時にそのときの事を思い出し、「あっ、コレは！？」と思わず呟いてしまいました。いやはや、使うこともないだろうと思ってすっかり忘れかけていたものをこの本がきっかけで再び思い出してしまいました。なんとも、なんとも。
「ある本」とは小難しい数学書なんかではなく勿論、「涼宮ハルヒの暴走」のことなのですよ。ッハハ。



X（頂点）+Y（面）-Z（辺）=D-1（次元-1）
■ 二次元 ■ 三次元
◎単体：「X+Y-Z=1」 ◎単体：「X+Y-Z=2」
4+1-4
=1		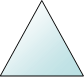 3+1-3
=1		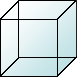 8+6-12
=2		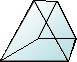 6+5-9
=2
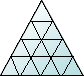15+16-30
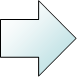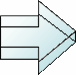
=1		 7+1-7
=1		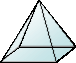 5+5-8
=2		 14+9-21
=2
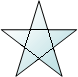
10+1-10
=1		 10+6-15
=1		 16+10-24
=2		 40+22-60
=2
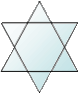12+7-18
=1		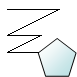 10+1-10
=1		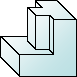 20+12-30
=2
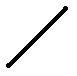↑ この二つは見にくくなるので実際に見える部分のみ線を書きました。
←
2+0-1
=1		 5+0-4
=1
9+4-12
=1		 9+0-8
=1
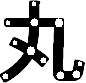11+0-10
=1		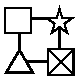 27+8-34
=1
↑ 丸抜きした部分を頂点とみる
◎複数（2個）：「（X+Y-Z）+（X+Y-Z）=2」 ◎複数（2個）：「（X+Y-Z）+（X+Y-Z）=4」
（2+0-1）+（2+0-1）
=2
（6+0-5）+（6+0-5）
=2
（6+1-6）+（6+2-7）
=2
（4+1-4）+（3+1-3）
=2
（4+1-4）+（5+4-8）
=2
（9+0-8）+（9+0-8）
=2
（9+4-12）+（8+2-9）
=2
（8+6-12）+（8+6-12）
=4
（20+12-30）+（5+5-8）
=4
◎複数（3個）：「（X+Y-Z）+（X+Y-Z）+（X+Y-Z）=3」 ◎複数（3個）：「（X+Y-Z）+（X+Y-Z）+（X+Y-Z）=6」
（6+0-5）+（2+0-1）+（4+1-4）
=3
（6+1-6）+（2+0-1）+（6+0-5）
=3
（4+1-4）+（4+1-4）+（4+1-4）
=3
（4+1-4）+（10+1-10）+（5+0-4）
=3
（2+0-1）+（2+0-1）+（3+1-3）
=3
（9+4-12）+（8+2-9）+（15+3-17）
=3
（8+6-12）+（8+6-12）+（8+6-12）
=6
（20+12-30）+（5+5-8）+（8+6-12）
=6
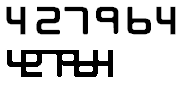← 図形としては「427964」は計6つですが、それらをくっつけると1つと考えることができます。

上：（5+0-4）+（6+0-5）+（3+0-2）+（5+1-5）+（5+1-5）+（5+0-4）=6
下：（20+3-22）=1

→ 結果：円と球を除いたものならばどんな図形でもこの式が成り立つようですね。
・・・じゃあ、円と球は？ってことで。

円は？
頂点：0、面：1、辺：1なので．．．0+1-1=0か？
球は？
頂点：0、面：1、辺：0だよな．．．ってことは0+1-0=1か？
→ ってことは円、球における関係式は「X+Y-Z=D-2」なのか？
誰か知ってる人いたらぜひ教えていただきたい。